Linear regression

• Linear regression 線性迴歸
• Simple Linear Regression 簡單線性迴歸
  • summary()
  • Residaul
• Multiple Regression
• R 範例

今天我們就要開始講到機器學習的模型了，那首先就從「線性迴歸」開始吧!

以線性迴歸的概念為基本，延伸了後續許多機器學習的方法，所以「線性迴歸」是一個很適合的開頭~

Linear regression 線性迴歸

迴歸分析主要是透過 OLS ( Ordinary least squares ) 最小化殘差平方( RSS, Minimized residual sum of square)或最大概似估計 ( MLE, Maximum likelihood estimation)的方式，計算出 ，獲得相對於資料較低偏差 ( Bias ) 和低變異 ( Variability ) 的函數，建立出一條能夠代表所有觀測資料的迴歸估計式。然後我們就可以藉由迴歸估計式來解釋關係性或是預測數值。

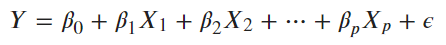
注意!

⇒ 在進行迴歸分析前，記得要排除離群值，這樣才能配釋出適合的迴歸估計式。

⇒ 迴歸分析只適用於 n >> p 資料數 n 大於解釋變數數目 p 的時候。

• 資料數若是接近解釋變數數目，容易造成過度擬合 ( overfitting ) 。
• 若是 n 小於 p ，則會產生計算錯誤，或是變異數非常大的情形。

當我們有太多解釋變數，或是解釋變數之間有高度相關時，我們可以考慮以下幾種解決方法:

• Subset Selection 變數篩選
• Shrinkage 收縮
• Dimension reduction 降維

這些方法會在下一篇討論~

1. Simple Linear Regression

介紹線性回歸的應用時，會先從簡單線性回歸的建模介紹起。
當我們覺得解釋變數 (X) 跟反應變數 (Y) 的關係呈現線性時我們可以試著去建立簡單線性回歸模型。計算出參數的估計係數後，我們能得知解釋變數 (X) 跟反應變數 (Y) 的關係，和它們之間的相關性(正、負相關)與相關程度。

lm(y ~ x , data) 是 R 裡內建的 Linear Model 的線性模型函數。 y 是我們的反映變數(Target, Label)， y 則是解釋變數 ( Variables )。 對應到的統計模型為 ， 是服從常態分佈 的殘差。

跑完線性模型函數後，我們可以使用summary()得到這個迴歸模型的報表結果。

• summary( )

lm.fit <-lm(medv ~lstat ,data=Boston) # lm() Simple Linear Regression
summary(lm.fit)

> lm.fit <-lm(medv ~lstat ,data=Boston)
> summary(lm.fit)

Call:
lm(formula = medv ~ lstat, data = Boston)

Residuals:
    Min      1Q  Median      3Q     Max 
-15.168  -3.990  -1.318   2.034  24.500 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 34.55384    0.56263   61.41   <2e-16 ***
lstat       -0.95005    0.03873  -24.53   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 6.216 on 504 degrees of freedom
Multiple R-squared:  0.5441,	Adjusted R-squared:  0.5432 
F-statistic: 601.6 on 1 and 504 DF,  p-value: < 2.2e-16

• model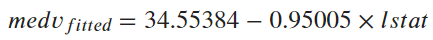
  

• t value

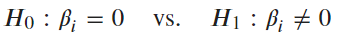
summary()的報表中，變數對應到的 t value 和 Pr(> | t | ) 是在進行 T 檢定，檢定某解釋變數的係數是否為零，當 p-value 顯著時，代表這個係數去有影響性。
***表達出變數的顯著程度。

• R-squared

Multiple R-squared 和 Adjusted R-squared 表達這個模型適不適合這份資料，通常希望能夠高於0.8。以這個簡單線性回歸的例子來說，兩種 R-squared 都太低了，模型並不適合，可能需要加入更多的解釋變數去改善模型。

• F-statistic

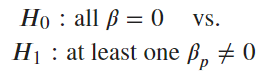
F-statistic則是在檢定是否所有解釋變數的係數都為零，當 p-value 顯著時，代表至少有一個解釋變數的係數不為零。

• Residaul

注意!
建立線性回歸時，必須要檢驗殘差(Residaul)是否符合以下三個假設：

• 常態性 ( Normality )
• 獨立性 ( Independence )
• 變異數同質性 ( Homogeneity of Variance )

model<-lm(y ~ x , data) #配適模型
model$residual #可以呼叫出殘差的值

#虛無假設H0:殘差服從常態分配
shapiro.test(model$residual) #檢驗殘差的常態性假設

#虛無假設H0:殘差間相互獨立
require(car) #car package
durbinWatsonTest(model) #檢驗殘差的獨立性

#虛無假設H0:殘差變異數具有同質性
require(car) #car package
ncvTest(model)#檢驗殘差的變異數同質性

#car package會自動計算模型中的殘差，故放入的是模型。

以上任一檢驗的p-value<0.05 時，拒絕，這表示配適的線性模型並不適合。

2. Multiple Regression

通常我們拿到資料往往不只有一個變數，甚至不是線性的關係，所以除了簡單線性回歸我們也可以試著去配適多元線性回歸去了解解釋變數(X)跟反應變數(Y)的函數關係。
以下是依些基礎的多元回歸模型示範程式碼:

指令函示	對應模型	解釋
lm(y ~ x , data)		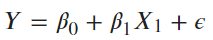簡單線性回歸
lm(y ∼ x1 + x2 + x3, data)
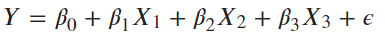lm(y ∼ . , data)		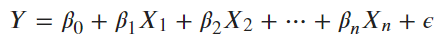放入所有解釋變數
lm(y ∼ . – x1 , data)		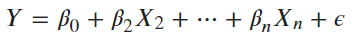所有解釋變數除了x1
lm(y ∼ x1 * x2 , data)		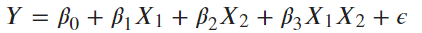加入交互作用項

R範例

以Boston dataset 作為示範，觀察資料:

## Boston dataset
install.packages("MASS") # Install packages 取得 Boston dataset
library(MASS)
data(Boston)
head(Boston)

> head(Boston)
     crim zn indus chas   nox    rm  age    dis rad tax ptratio  black lstat
1 0.00632 18  2.31    0 0.538 6.575 65.2 4.0900   1 296    15.3 396.90  4.98
2 0.02731  0  7.07    0 0.469 6.421 78.9 4.9671   2 242    17.8 396.90  9.14
3 0.02729  0  7.07    0 0.469 7.185 61.1 4.9671   2 242    17.8 392.83  4.03
4 0.03237  0  2.18    0 0.458 6.998 45.8 6.0622   3 222    18.7 394.63  2.94
5 0.06905  0  2.18    0 0.458 7.147 54.2 6.0622   3 222    18.7 396.90  5.33
6 0.02985  0  2.18    0 0.458 6.430 58.7 6.0622   3 222    18.7 394.12  5.21
  medv
1 24.0
2 21.6
3 34.7
4 33.4
5 36.2
6 28.7

1. 首先示範簡單線性回歸

lm.fit <-lm(medv ~lstat ,data=Boston) # lm() Simple Linear Regression
summary(lm.fit)
coef(lm.fit) # coefficients可以單獨回傳估計係數值

## 紅色的簡單線性回歸模型配適曲線與資料點的分布情形
plot (Boston$lstat, Boston$medv) 
abline (lm.fit,col="red")

## 模型的殘差
plot(predict(lm.fit), residuals(lm.fit)) 

2. 多元線性回歸

## Multiple Linear Regression
lm.fit1 <- lm(medv ~ ., data = Boston)
summary(lm.fit1)

lm.fit2 <- lm(medv ~ . - age, data = Boston)
summary(lm.fit2)

lm.fit3 <- lm(medv ~ lstat * age , data = Boston) # Interaction Terms
summary (lm.fit3)

3. 使用模型預測新資料

• predict( fit.model, new.x )

lm.fit <-lm(medv ~lstat ,data=Boston)
predict(lm.fit,data.frame(lstat = (c(5, 10, 15)))) # 將新資料 lstat=5, 10, 15代入模型中進行預測，回傳預測的 medv 值

以上就是 Linear Regression 在 R 上的基本操作與結果判讀。

其他額外補充

如果今天有報告需求，需要展示模型結果然後又想要整齊的輸出畫面時，可以試試stargazer套件。

install.packages("stargazer")
library(stargazer)

library(MASS) # Boston data
model <-lm(medv ~lstat ,data=Boston) 
stargazer(model, type="text") # type = "latex", "html", "text"

輸出類型包含默認值 LaTeX code "latex"、 HTML/CSS code "html"和 ASCII text output "text"。

===============================================
                        Dependent variable:    
                    ---------------------------
                               medv            
-----------------------------------------------
lstat                        -0.950***         
                              (0.039)          
                                               
Constant                     34.554***         
                              (0.563)          
                                               
-----------------------------------------------
Observations                    506            
R2                             0.544           
Adjusted R2                    0.543           
Residual Std. Error      6.216 (df = 504)      
F Statistic          601.618*** (df = 1; 504)  
===============================================
Note:               *p<0.1; **p<0.05; ***p<0.01

參考來源:https://wangcc.me/LSHTMlearningnote/lm.html

參考資料、網站及書籍

統計與機器學習 Statistical and Machine Learning 課程

R筆記–(5)初聲試啼-簡單的資料分析(迴歸分析) (@skydome20)
https://rpubs.com/skydome20/R-Note5-First_Practice
簡單線性迴歸 Simple Linear Regression (@Chaochen Wang)
https://wangcc.me/LSHTMlearningnote/lm.html

An Introduction to Statistical Learning with Applications in R. 2nd edition. Springer. James, G., Witten, D., Hastie, T., and Tibshirani, R. (2021).